Rotacional

En el cálculo vectorial, el rotacional o rotor es un operador vectorial sobre campos vectoriales definidos en un intervalo abierto de ${\displaystyle \mathbb {R} ^{3}}$ que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto.

Matemáticamente, esta idea se expresa como el límite de la circulación del campo vectorial, cuando la curva sobre la que se integra se reduce a un punto:

${\displaystyle \mathbf {U} \cdot {\mbox{rot}}\ \mathbf {F} =\mathbf {U} \cdot \nabla \times \mathbf {F} \equiv \lim _{\Delta S\to 0}{\frac {1}{\Delta S}}\oint _{C}\mathbf {F} \cdot {\text{d}}\mathbf {r} }$

Aquí, ${\displaystyle \Delta S}$ es el área de la superficie apoyada en la curva ${\displaystyle C}$, que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a ${\displaystyle \Delta S}$ y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.

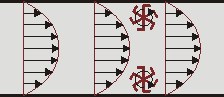
Aunque el que el rotacional de un campo alrededor de un punto sea distinto de cero no implica que las líneas de campo giren alrededor de ese punto y lo encierren. Por ejemplo, el campo de velocidades de un fluido que circula por una tubería (conocido como perfil de Poiseuille) posee un rotacional no nulo en todas partes, salvo en el eje central, pese a que la corriente fluye en línea recta:

La idea es que si colocamos una rueda de paletas infinitamente pequeña en el interior del campo vectorial, esta rueda girará, aunque el campo tenga siempre la misma dirección, debido a la diferente magnitud del campo a un lado y a otro de la rueda.