
Back Сплайн Bulgarian Spline Czech Spline German Spline (mathematics) English Splajno Esperanto Spline Spanish Splain Estonian اسپلاین (ریاضیات) Persian Spline French Spline Galician
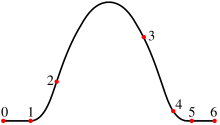

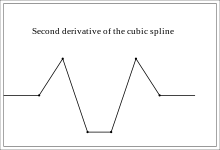
En matemàtiques, un spline (o traçador) és una funció polinòmica definida a trossos que interpola una sèrie de punts de forma que cada tros és un polinomi de grau n i a cada punt les derivades dels dos trossos que hi connecten tenen iguals les seves derivades fins a l'ordre n-1.
En problemes d'interpolació, la interpolació per splines es preferix sovint a la interpolació polinòmica perquè produeix resultats similars, fins i tot quan es fan servir polinomis de grau baix, mentre que evita el fenomen de Runge que apareix quan s'empren polnomis de graus alts
En infografia els splines són corbes emprades amb freqüència perquè són fàcils per traçar i precises, per poder avaluar les funcions que els defineixen, i també perquè permeten aproximar formes complexes amb les tècniques d'ajust de corbes i de disseny interactiu de corbes.
El terme spline ve dels regles flexibles emprats pels constructors de vaixells i els dissenyadors industrials per dibuixar corbes.
Els splines que es fan servir més són els splines cúbics, és a dir d'ordre 3 en particular els B-splines 3 i els splines de Bézier cúbics. Són comuns, en particular, en interpolació per splines que simula la funció del regle flexible.