Calcwlws differol

Calcwlws differol

Enghraifft o'r canlynol	maes o fewn mathemateg
Math	calcwlws
Y gwrthwyneb	Calcwlws integrol
Ffeiliau perthnasol ar Gomin Wicimedia

O fewn mathemateg mae calcwlws differol yn un o is-feysydd calcwlws,^[1] ac yn astudiaeth o'r raddfa mae meintiau'n newid.

Dau raniad clasurol sydd i galcwlws: calcwlws differol yw'r naill a chalcwlws integrol, sef yr astudiaeth o'r ardal o dan cromlin, yw'r llall.^[2] Cysylltir y ddau raniad hyn gan theoremau ffwndamental calcwlws, sy'n mynnu mai differiad yw'r gwrthwyneb i'r integriad (integration).^[3]

Mesur o sut mae ffwythiant mathemategol yn newid wrth i'r mewnbynnau newid yw differu - y weithred o gyfrifo'r deilliant. Y prif wrthrychau, neu feysydd a astudir o fewn calcwlws differol yw deilliannau'r ffwythiant a syniadau perthnasol megis differynnau (differential) a sut maent yn cael eu cymhwyso ymhellach, ac o ddydd i ddydd.^[4]

Mae deillaint y ffwythiant, felly, o unrhyw werth a fewnbynir yn ddisgrifiad o raddfa newid y ffwythiant ger y fan honno (y gwerth mewnbwn). Gelwir y broses o ganfod y deilliant yn "ddifferiad" (differentiation).

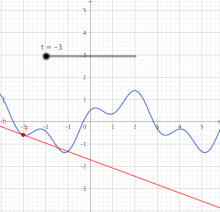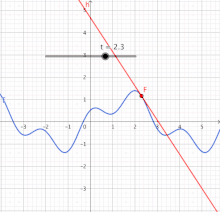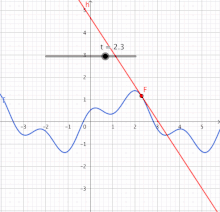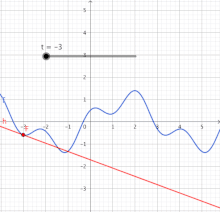
O ran geometreg, y linell dangiad yw'r brasamcan gorau o'r ffwythiant ger gwerth y mewnbwn (gw. y diagram ar y dde, uchod). Oherwydd hyn, disgrifir y deilliant yn aml fel "graddfa'r newid ar un amrantiad o amser". O ran ffwythiant gwerth-real o newidyn real, deilliant y ffwythiant ar bwynt arbennig sydd fel arfer yn penderfynnu'r brasamcan gorau i'r ffwythiant ar y pwynt hwnnw.

1. ↑ "Definition of DIFFERENTIAL CALCULUS". www.merriam-webster.com (yn Saesneg). Cyrchwyd 2018-09-26.
2. ↑ ""Integral Calculus - Definition of Integral calculus by Merriam-Webster"". www.merriam-webster.com (yn Saesneg). Cyrchwyd 2018-05-01.
3. ↑ geiriadur.bangor.ac.uk; Y Termiadur Addysg - Daearyddiaeth a Daeareg, Ffiseg a Mathemateg; adalwyd 8 Rhagfyr 2018.
4. ↑ geiriadur.bangor.ac.uk; Y Termiadur Addysg - Daearyddiaeth a Daeareg, Ffiseg a Mathemateg; adalwyd 8 Rhagfyr 2018.