
Back مستطيل ذهبي Arabic لاکێشەی زێڕین CKB Ылттăн тӳркĕтеслĕх CV Goldenes Rechteck German Golden rectangle English Ora ortangulo Esperanto Rectángulo dorado Spanish Kultainen suorakulmio Finnish Rectángulo dourado Galician स्वर्णिमायत Hindi

Et gyldent rektangel er et rektangel hvis proportioner svarer til det gyldne snit, 1 : φ (dvs., 1 : 1,618... ). Figuren påstås at være det æstetisk mest behagelige rektangel.
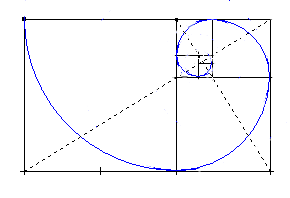
En karakteristisk egenskab ved denne figur er, at man, hvis man fjerner den kvadratiske del af et gyldent rektangel, står tilbage med endnu et nyt gyldent rektangel med samme proportioner som det første. Denne proces kan gentages i det uendelige, hvilket fører til en approksimation af den gyldne spiral.
Nautil-sneglens hus siges ofte fejlagtigt at være opbygget efter den gyldne spiral. Det er opbygget efter en logaritmisk spiral; men ikke nødvendigvis den gyldne spiral.