Tetraeder

Tetraeder
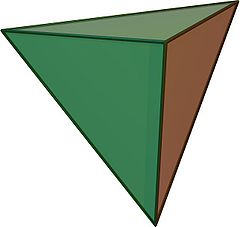Klik på billedet for større version. Klik her for omdrejende version.
Type	Platonisk
Sideflade	trekant
Sideflader	4
Kanter	6
Hjørner	4
Sideflader ved hvert hjørne	3
Hjørner ved hver sideflade	3
Symmetrigruppe	tetraedralsk (Td)
Dualt polyeder	tetraeder (selvdual)
Dihedralsk vinkel	70° 32'
Egenskaber	regulær, konveks

Et tetraeder (flertal: tetraedre) er et polyeder hvis fire sideflader er trekanter, af hvilke tre mødes ved hvert hjørne. Et regulært tetraeder er et hvori de fire trekanter er ligesidede, og er et af de platoniske legemer.

Et tetraeder kan som et hvert andet polyeder udfoldes af et enkelt stykke papir.

Arealet, A, og volumenet, V, af et regulært tetraeder af sidelængden a er:

${\displaystyle A={\sqrt {3}}a^{2}}$

${\displaystyle V={\begin{matrix}{1 \over 12}\end{matrix}}{\sqrt {2}}a^{3}}$

Et tetraeder er et 3-simpleks.

Tetraedre er en særlig type af triangulære pyramider, og er selvdual. De kanoniske koordinater for hjørnerne af den regulære tetraeder er (1, 1, 1), (-1, -1, 1), (-1, 1, -1) og (1, -1, -1). Et regulært tetraeder kan indskrives i en terning på to måder, sådan at hvert hjørne svarer til terningens hjørne, og hver diagonal er en diagonal i terningens sideflader. Volumenet af dette tetraeder er 1/3 af terningens volumen. Ved at tage begge tetraedre indenfor en enkelt terning får man en regulær polyedisk sammensætning, som benævnes stella oktangula, og som har et oktaeder som masse. Indskrivning af tetraedre i den regulære sammensætning af fem terninger giver to yderligere regulære sammensætninger, som består af fem og ti tetraedre.

Regulære tetraedre kan ikke i sig selv "udfylde" rummet, selv om det virker sandsynligt nok, at Aristoteles erklærede at det var muligt. I virkeligheden er oktaedre nødvendige for at udfylde nogle af mellemrummene. Dette er også én af de fem Andreini dækninger (?), og er et begrænsende tilfælde af et andet, et "dækning" der involverer tetraeder og beskårede tetraedre.

Volumenet af et irregulært tetraeder, givet dens sidelængder a, b, c og d, er (1/6)·|det(a-b, b-c, c-d)|, eller en hvilken som helst anden kombination af par af sidelængder som danner en enkeltsammensat graf. Dette gælder naturligvis også for regulære tetraedre.

Som alle platoniske legemer, archimediske legemer og endda alle konvekse polyedre, kan et tetraeder foldes fra et enkelt stykke papir.

Tetraeder-formede terninger anvendes i rollespilssammenhæng og kaldes da ofte d4 (fra engelsk die: terning).