
Back انسحاب (هندسة) Arabic Транслация Bulgarian Translació (geometria) Catalan Posunutí (geometrie) Czech Параллеллĕ куçару CV Translation (geometri) Danish Translation (geometry) English Translacio (geometrio) Esperanto Traslación (geometría) Spanish Rööplüke Estonian
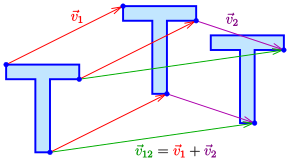
Die Hintereinanderausführung zweier Translationen ist wieder eine Translation.
Die Parallelverschiebung oder Translation ist eine geometrische Abbildung, die jeden Punkt der Zeichenebene oder des Raumes in dieselbe Richtung um dieselbe Strecke verschiebt. Sie kann durch einen Vektor, den sogenannten Verschiebungsvektor, gekennzeichnet werden.
Parallelverschiebungen gehören zu den Bewegungen, da bei ihrer Anwendung Längen und Winkel erhalten bleiben. Als Bewegungen werden sie – vor allem die Parallelverschiebungen in der Ebene – auch zu den Kongruenzabbildungen gezählt.
Der Begriff der Parallelverschiebung kann aus dem zwei- oder dreidimensionalen Anschauungsraum in den n-dimensionalen euklidischen Raum und noch weiter in die riemannsche Geometrie oder die affine Geometrie verallgemeinert werden.