Back نقطة متقابلة Arabic Antipode (Mathematik) German Αντιδιαμετρικό σημείο Greek Punto antipodal Spanish نقطه پادپایی Persian Punti antipodali (matematica) Italian Ponto antipodal Portuguese Punct antipodal Romanian Антиподална тачка Serbian Điểm đối cực Vietnamese

Antipodal point

For the geographical antipodal point of a place on Earth, see antipodes.
The two points P and P' (red) are antipodal because they are ends of a diameter PP', a segment of the axis a (purple) passing through the sphere's center O (black). P and P' are the poles of a great circle g (green) whose points are equidistant from each (with a central right angle). Any great circle s (blue) passing through the poles is secondary to g.

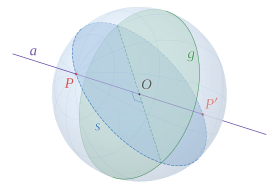
In mathematics, two points of a sphere (or n-sphere, including a circle) are called antipodal or diametrically opposite if they are the endpoints of a diameter, a straight line segment between two points on a sphere and passing through its center.[1]

Given any point on a sphere, its antipodal point is the unique point at greatest distance, whether measured intrinsically (great-circle distance on the surface of the sphere) or extrinsically (chordal distance through the sphere's interior). Every great circle on a sphere passing through a point also passes through its antipodal point, and there are infinitely many great circles passing through a pair of antipodal points (unlike the situation for any non-antipodal pair of points, which have a unique great circle passing through both). Many results in spherical geometry depend on choosing non-antipodal points, and degenerate if antipodal points are allowed; for example, a spherical triangle degenerates to an underspecified lune if two of the vertices are antipodal.

The point antipodal to a given point is called its antipodes, from the Greek ἀντίποδες (antípodes) meaning "opposite feet"; see Antipodes § Etymology. Sometimes the s is dropped, and this is rendered antipode, a back-formation.

  1. ^ Chisholm, Hugh, ed. (1911). "Antipodes" . Encyclopædia Britannica. Vol. 2 (11th ed.). Cambridge University Press. pp. 133–34.

Developed by StudentB