Archimedean spiral

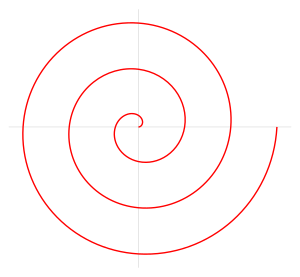
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Greek mathematician Archimedes. The term Archimedean spiral is sometimes used to refer to the more general class of spirals of this type (see below), in contrast to Archimedes' spiral (the specific arithmetic spiral of Archimedes). It is the locus corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line that rotates with constant angular velocity. Equivalently, in polar coordinates (r, θ) it can be described by the equation $${\displaystyle r=b\cdot \theta }$$ with real number b. Changing the parameter b controls the distance between loops.

From the above equation, it can thus be stated: position of the particle from point of start is proportional to angle θ as time elapses.

Archimedes described such a spiral in his book On Spirals. Conon of Samos was a friend of his and Pappus states that this spiral was discovered by Conon.^[1]