
Back توزيع برنولي Arabic Bernulli paylanması Azerbaijani Размеркаванне Бернулі Byelorussian Distribució de Bernoulli Catalan Alternativní rozdělení Czech Bernoulli-Verteilung German Κατανομή Μπερνούλλι Greek Distribución Bernoulli Spanish Bernoulliren banaketa Basque توزیع برنولی Persian
|
Probability mass function 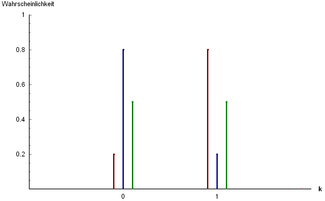
Three examples of Bernoulli distribution: and
and
and | |||
| Parameters |
| ||
|---|---|---|---|
| Support | |||
| PMF | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| MAD | |||
| Skewness | |||
| Excess kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | |||
| PGF | |||
| Fisher information | |||
| Part of a series on statistics |
| Probability theory |
|---|
 |
In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli,[1] is the discrete probability distribution of a random variable which takes the value 1 with probability and the value 0 with probability . Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question. Such questions lead to outcomes that are Boolean-valued: a single bit whose value is success/yes/true/one with probability p and failure/no/false/zero with probability q. It can be used to represent a (possibly biased) coin toss where 1 and 0 would represent "heads" and "tails", respectively, and p would be the probability of the coin landing on heads (or vice versa where 1 would represent tails and p would be the probability of tails). In particular, unfair coins would have
The Bernoulli distribution is a special case of the binomial distribution where a single trial is conducted (so n would be 1 for such a binomial distribution). It is also a special case of the two-point distribution, for which the possible outcomes need not be 0 and 1. [2]
- ^ Uspensky, James Victor (1937). Introduction to Mathematical Probability. New York: McGraw-Hill. p. 45. OCLC 996937.
- ^ Dekking, Frederik; Kraaikamp, Cornelis; Lopuhaä, Hendrik; Meester, Ludolf (9 October 2010). A Modern Introduction to Probability and Statistics (1 ed.). Springer London. pp. 43–48. ISBN 9781849969529.












![{\displaystyle {\begin{cases}0&{\text{if }}p<1/2\\\left[0,1\right]&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/482cc0f5f8c739e3fe2462d72ee5b9f1f7b5d5a4)










