
Back توزيع ثنائي الحدين Arabic Distribución binómica AST Біномнае размеркаванне Byelorussian দ্বিপদী বন্টন Bengali/Bangla Distribució binomial Catalan Binomické rozdělení Czech Binomialfordelingen Danish Binomialverteilung German Διωνυμική κατανομή Greek Distribución binomial Spanish
|
Probability mass function 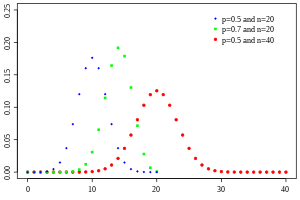 | |||
|
Cumulative distribution function 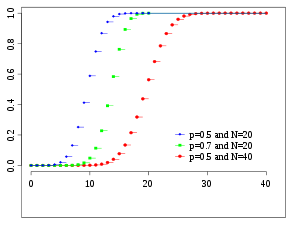 | |||
| Notation | |||
|---|---|---|---|
| Parameters |
– number of trials – success probability for each trial | ||
| Support | – number of successes | ||
| PMF | |||
| CDF | (the regularized incomplete beta function) | ||
| Mean | |||
| Median | or | ||
| Mode | or | ||
| Variance | |||
| Skewness | |||
| Excess kurtosis | |||
| Entropy |
in shannons. For nats, use the natural log in the log. | ||
| MGF | |||
| CF | |||
| PGF | |||
| Fisher information |
(for fixed ) | ||
| Part of a series on statistics |
| Probability theory |
|---|
 |

with n and k as in Pascal's triangle
The probability that a ball in a Galton box with 8 layers (n = 8 ends up in the central bin (k = 4 is 70/256.
In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success (with probability p) or failure (with probability q = 1 − p). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the binomial test of statistical significance.[1]
The binomial distribution is frequently used to model the number of successes in a sample of size n drawn with replacement from a population of size N. If the sampling is carried out without replacement, the draws are not independent and so the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution remains a good approximation, and is widely used.
- ^ Westland, J. Christopher (2020). Audit Analytics: Data Science for the Accounting Profession. Chicago, IL, USA: Springer. p. 53. ISBN 978-3-030-49091-1.


![{\displaystyle p\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33c3a52aa7b2d00227e85c641cca67e85583c43c)















![{\displaystyle G(z)=[q+pz]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40494c697ce2f88ebb396ac0191946285cadcbdd)

