Colossally abundant number

In number theory, a colossally abundant number (sometimes abbreviated as CA) is a natural number that, in a particular, rigorous sense, has many divisors. Particularly, it is defined by a ratio between the sum of an integer's divisors and that integer raised to a power higher than one. For any such exponent, whichever integer has the highest ratio is a colossally abundant number. It is a stronger restriction than that of a superabundant number, but not strictly stronger than that of an abundant number.

Formally, a number n is said to be colossally abundant if there is an ε > 0 such that for all k > 1,

${\displaystyle {\frac {\sigma (n)}{n^{1+\varepsilon }}}\geq {\frac {\sigma (k)}{k^{1+\varepsilon }}}}$

where σ denotes the sum-of-divisors function.^[1]

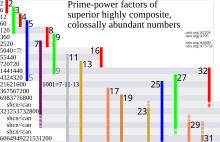
The first 15 colossally abundant numbers, 2, 6, 12, 60, 120, 360, 2520, 5040, 55440, 720720, 1441440, 4324320, 21621600, 367567200, 6983776800 (sequence A004490 in the OEIS) are also the first 15 superior highly composite numbers, but neither set is a subset of the other.