Contour line

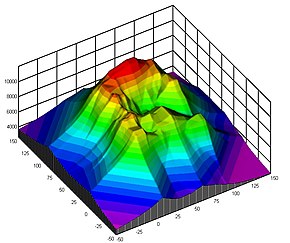
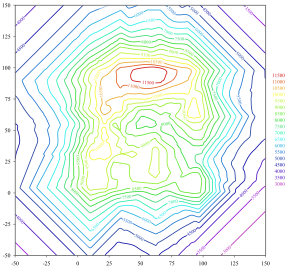
A contour line (also isoline, isopleth, isoquant or isarithm) of a function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value.^[1][2] It is a plane section of the three-dimensional graph of the function ${\displaystyle f(x,y)}$ parallel to the ${\displaystyle (x,y)}$-plane. More generally, a contour line for a function of two variables is a curve connecting points where the function has the same particular value.^[2]

In cartography, a contour line (often just called a "contour") joins points of equal elevation (height) above a given level, such as mean sea level.^[3] A contour map is a map illustrated with contour lines, for example a topographic map, which thus shows valleys and hills, and the steepness or gentleness of slopes.^[4] The contour interval of a contour map is the difference in elevation between successive contour lines.^[5]

The gradient of the function is always perpendicular to the contour lines. When the lines are close together the magnitude of the gradient is large: the variation is steep. A level set is a generalization of a contour line for functions of any number of variables.

Contour lines are curved, straight or a mixture of both lines on a map describing the intersection of a real or hypothetical surface with one or more horizontal planes. The configuration of these contours allows map readers to infer the relative gradient of a parameter and estimate that parameter at specific places. Contour lines may be either traced on a visible three-dimensional model of the surface, as when a photogrammetrist viewing a stereo-model plots elevation contours, or interpolated from the estimated surface elevations, as when a computer program threads contours through a network of observation points of area centroids. In the latter case, the method of interpolation affects the reliability of individual isolines and their portrayal of slope, pits and peaks.^[6]