
Back E (wiskunde) Afrikaans ኦይለር ቁጥር Amharic Numero e AN ه (رياضيات) Arabic Númberu e AST E (ədəd) Azerbaijani Е (һан) Bashkir E (лік) Byelorussian Неперово число Bulgarian অয়লারের ধ্রুবক Bengali/Bangla
| Euler's number | |
|---|---|
| e 2.71828...[1] | |
| General information | |
| Type | Transcendental |
| History | |
| Discovered | 1685 |
| By | Jacob Bernoulli |
| First mention | Quæstiones nonnullæ de usuris, cum solutione problematis de sorte alearum, propositi in Ephem. Gall. A. 1685 |
| Named after | |
| Part of a series of articles on the |
| mathematical constant e |
|---|
 |
| Properties |
| Applications |
| Defining e |
| People |
| Related topics |
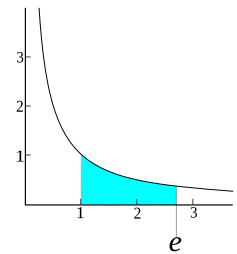
The number e is a mathematical constant approximately equal to 2.71828 that is the base of the natural logarithm and exponential function. It is sometimes called Euler's number, after the Swiss mathematician Leonhard Euler, though this can invite confusion with Euler numbers, or with Euler's constant, a different constant typically denoted . Alternatively, e can be called Napier's constant after John Napier.[2][3] The Swiss mathematician Jacob Bernoulli discovered the constant while studying compound interest.[4][5]
The number e is of great importance in mathematics,[6] alongside 0, 1, π, and i. All five appear in one formulation of Euler's identity and play important and recurring roles across mathematics.[7][8] Like the constant π, e is irrational, meaning that it cannot be represented as a ratio of integers, and moreover it is transcendental, meaning that it is not a root of any non-zero polynomial with rational coefficients.[3] To 30 decimal places, the value of e is:[1]
- ^ a b Sloane, N. J. A. (ed.). "Sequence A001113 (Decimal expansion of e)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Cite error: The named reference
Millerwas invoked but never defined (see the help page). - ^ a b Weisstein, Eric W. "e". mathworld.wolfram.com. Retrieved 2020-08-10.
- ^ Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (illustrated ed.). Sterling Publishing Company. p. 166. ISBN 978-1-4027-5796-9. Extract of page 166
- ^ O'Connor, John J.; Robertson, Edmund F. (September 2001). "The number e". MacTutor History of Mathematics Archive. University of St Andrews.
- ^ Sawyer, W. W. (1961). Mathematician's Delight. Penguin. p. 155.
- ^ Wilson, Robinn (2018). Euler's Pioneering Equation: The most beautiful theorem in mathematics (illustrated ed.). Oxford University Press. p. (preface). ISBN 978-0-19-251405-9.
- ^ Posamentier, Alfred S.; Lehmann, Ingmar (2004). Pi: A Biography of the World's Most Mysterious Number (illustrated ed.). Prometheus Books. p. 68. ISBN 978-1-59102-200-8.

