Epsilon

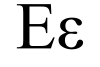Greek alphabet
Αα Alpha Νν Nu Ββ Beta Ξξ Xi Γγ Gamma Οο Omicron Δδ Delta Ππ Pi Εε Epsilon Ρρ Rho Ζζ Zeta Σσς Sigma Ηη Eta Ττ Tau Θθ Theta Υυ Upsilon Ιι Iota Φφ Phi Κκ Kappa Χχ Chi Λλ Lambda Ψψ Psi Μμ Mu Ωω Omega
History
Archaic local variants Ϝ Digamma Ͱ Heta Ϻ San Ϙ Koppa Ͷ Tsan Digamma Ͳ Sampi
Diacritics and other symbols
Diacritics ά ὰ ᾶ ἀ ἁ ᾱ ᾰ ϊ ᾳ σ̌ Ligatures ϗ ϛ Numerals (Attic) ϛ (6) ϟ (90) ϡ (900)
Related topics
Use as scientific symbols Orthography Romanization Cyrillization
Category
v t e

Epsilon (US: /ˈɛpsɪlɒn/,^[1] UK: /ɛpˈsaɪlən/;^[2] uppercase Ε, lowercase ε or ϵ; Greek: έψιλον) is the fifth letter of the Greek alphabet, corresponding phonetically to a mid front unrounded vowel IPA: [e̞] or IPA: [ɛ̝]. In the system of Greek numerals it also has the value five. It was derived from the Phoenician letter He . Letters that arose from epsilon include the Roman E, Ë and Ɛ, and Cyrillic Е, È, Ё, Є and Э. The name of the letter was originally εἶ (Ancient Greek: [êː]), but it was later changed to ἒ ψιλόν (e psilon 'simple e') in the Middle Ages to distinguish the letter from the digraph αι, a former diphthong that had come to be pronounced the same as epsilon.

The uppercase form of epsilon is identical to Latin ⟨E⟩ but has its own code point in Unicode: U+0395 Ε GREEK CAPITAL LETTER EPSILON. The lowercase version has two typographical variants, both inherited from medieval Greek handwriting. One, the most common in modern typography and inherited from medieval minuscule, looks like a reversed number "3" and is encoded U+03B5 ε GREEK SMALL LETTER EPSILON. The other, also known as lunate or uncial epsilon and inherited from earlier uncial writing,^[3][4] looks like a semicircle crossed by a horizontal bar: it is encoded U+03F5 ϵ GREEK LUNATE EPSILON SYMBOL. While in normal typography these are just alternative font variants, they may have different meanings as mathematical symbols: computer systems therefore offer distinct encodings for them.^[3] In TeX, \epsilon ( ${\displaystyle \epsilon \!}$ ) denotes the lunate form, while \varepsilon ( ${\displaystyle \varepsilon _{0}}$ ) denotes the epsilon number. Unicode versions 2.0.0 and onwards use ɛ as the lowercase Greek epsilon letter,^[5] but in version 1.0.0, ϵ was used.^[6] The lunate or uncial epsilon provided inspiration for the euro sign, €.^[7]

There is also a 'Latin epsilon', ⟨ɛ⟩ or "open e", which looks similar to the Greek lowercase epsilon. It is encoded in Unicode as U+025B ɛ LATIN SMALL LETTER OPEN E and U+0190 Ɛ LATIN CAPITAL LETTER OPEN E and is used as an IPA phonetic symbol. This Latin uppercase epsilon, Ɛ, is not to be confused with the Greek uppercase Σ (sigma)

The lunate epsilon, ⟨ϵ⟩, is not to be confused with the set membership symbol ∈. The symbol ${\displaystyle \in }$, first used in set theory and logic by Giuseppe Peano and now used in mathematics in general for set membership ("belongs to"), evolved from the letter epsilon, since the symbol was originally used as an abbreviation for the Latin word est. In addition, mathematicians often read the symbol ∈ as "element of", as in "1 is an element of the natural numbers" for ${\displaystyle 1\in \mathbb {N} }$, for example. As late as 1960, ɛ itself was used for set membership, while its negation "does not belong to" (now ∉) was denoted by ε' (epsilon prime).^[8] Only gradually did a fully separate, stylized symbol take the place of epsilon in this role. In a related context, Peano also introduced the use of a backwards epsilon, ϶, for the phrase "such that", although the abbreviation s.t. is occasionally used in place of ϶ in informal cardinals.