Exponential distribution

Exponential

Probability density function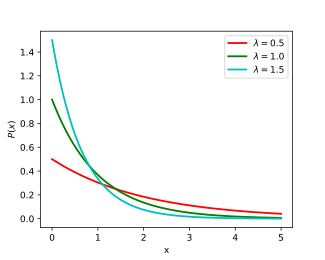
Cumulative distribution function
Parameters	${\displaystyle \lambda >0,}$ rate, or inverse scale
Support	${\displaystyle x\in [0,\infty )}$
PDF	${\displaystyle \lambda e^{-\lambda x}}$
CDF	${\displaystyle 1-e^{-\lambda x}}$
Quantile	${\displaystyle -{\frac {\ln(1-p)}{\lambda }}}$
Mean	${\displaystyle {\frac {1}{\lambda }}}$
Median	${\displaystyle {\frac {\ln 2}{\lambda }}}$
Mode	${\displaystyle 0}$
Variance	${\displaystyle {\frac {1}{\lambda ^{2}}}}$
Skewness	${\displaystyle 2}$
Excess kurtosis	${\displaystyle 6}$
Entropy	${\displaystyle 1-\ln \lambda }$
MGF	${\displaystyle {\frac {\lambda }{\lambda -t}},{\text{ for }}t<\lambda }$
CF	${\displaystyle {\frac {\lambda }{\lambda -it}}}$
Fisher information	${\displaystyle {\frac {1}{\lambda ^{2}}}}$
Kullback–Leibler divergence	${\displaystyle \ln {\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda }{\lambda _{0}}}-1}$
Expected shortfall	${\displaystyle {\frac {-\ln(1-p)+1}{\lambda }}}$

In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process.^[1] It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless.^[2] In addition to being used for the analysis of Poisson point processes it is found in various other contexts.^[3]

The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includes many other distributions, like the normal, binomial, gamma, and Poisson distributions.^[3]