
Back Formal qrammatika Azerbaijani Formalna gramatika BS Gramàtica formal Catalan Formální gramatika Czech Formale Grammatik German Τυπική γραμματική Greek Formala gramatiko Esperanto Gramática formal Spanish Formaalne grammatika Estonian دستور صوری Persian
| Part of a series on |
| Formal languages |
|---|
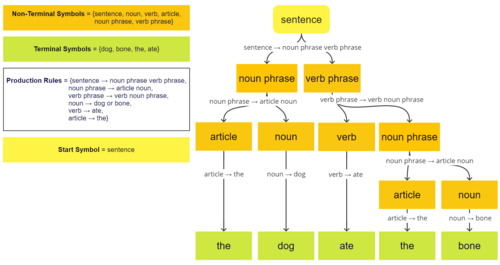
A formal grammar describes which strings from an alphabet of a formal language are valid according to the language's syntax. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form. A formal grammar is defined as a set of production rules for such strings in a formal language.
Formal language theory, the discipline that studies formal grammars and languages, is a branch of applied mathematics. Its applications are found in theoretical computer science, theoretical linguistics, formal semantics, mathematical logic, and other areas.
A formal grammar is a set of rules for rewriting strings, along with a "start symbol" from which rewriting starts. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatically incorrect. To describe such recognizers, formal language theory uses separate formalisms, known as automata theory. One of the interesting results of automata theory is that it is not possible to design a recognizer for certain formal languages.[1] Parsing is the process of recognizing an utterance (a string in natural languages) by breaking it down to a set of symbols and analyzing each one against the grammar of the language. Most languages have the meanings of their utterances structured according to their syntax—a practice known as compositional semantics. As a result, the first step to describing the meaning of an utterance in language is to break it down part by part and look at its analyzed form (known as its parse tree in computer science, and as its deep structure in generative grammar).
- ^ Meduna, Alexander (2014), Formal Languages and Computation: Models and Their Applications, CRC Press, p. 233, ISBN 9781466513457. For more on this subject, see undecidable problem.