Geometric series

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Geometric series" – news · newspapers · books · scholar · JSTOR (August 2024) (Learn how and when to remove this message)

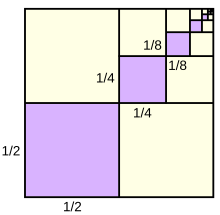
In mathematics, a geometric series is a series in which the ratio of successive adjacent terms is constant. In other words, the sum of consecutive terms of a geometric sequence forms a geometric series. Each term is therefore the geometric mean of its two neighbouring terms, similar to how the terms in an arithmetic series are the arithmetic means of their two neighbouring terms.

Geometric series have been studied in mathematics from at least the time of Euclid in his work, Elements, which explored geometric proportions. Archimedes further advanced the study through his work on infinite sums, particularly in calculating areas and volumes of geometric shapes (for instance calculating the area inside a parabola) and the early development of calculus, where they have been paradigmatic examples of both convergent series and divergent series. They serve as prototypes for frequently used mathematical tools such as Taylor series, Fourier series, and matrix exponentials.

Geometric series have been applied to model a wide variety of natural phenomena and social phenomena, such as the expansion of the universe where the common ratio between terms is defined by Hubble's constant, the decay of radioactive carbon-14 atoms where the common ratio between terms is defined by the half-life of carbon-14, probabilities of winning in games of chance where the common ratio could be determined by the odds of a roulette wheel, and the economic values of investments where the common ratio could be determined by a combination of inflation rates and interest rates.

In general, a geometric series is written as ${\displaystyle a+ar+ar^{2}+ar^{3}+...}$, where ${\displaystyle a}$ is the initial term and ${\displaystyle r}$ is the common ratio between adjacent terms. For example, the series

${\displaystyle {\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots }$

is geometric because each successive term can be obtained by multiplying the previous term by ${\displaystyle 1/2}$.

Truncated geometric series ${\displaystyle a+ar+ar^{2}+ar^{3}+\dots +ar^{n}}$ are called "finite geometric series" in certain branches of mathematics, especially in 19th century calculus and in probability and statistics and their applications.

The standard generator form^[1] expression for the infinite geometric series is

${\displaystyle a+ar+ar^{2}+ar^{3}+\dots =\sum _{k=0}^{\infty }ar^{k}}$

and the generator form expression for the finite geometric series is

${\displaystyle a+ar+ar^{2}+ar^{3}+\dots +ar^{n}=\sum _{k=0}^{n}ar^{k}.}$

Any finite geometric series has the sum ${\displaystyle a(1-r^{n+1})/(1-r)}$, and when ${\displaystyle |r|<1}$ the infinite series converges to the value ${\displaystyle a/(1-r)}$.

Though geometric series are most commonly found and applied with the real or complex numbers for ${\displaystyle a}$ and ${\displaystyle r}$, there are also important results and applications for matrix-valued geometric series, function-valued geometric series, p-adic number geometric series, and, most generally, geometric series of elements of abstract algebraic fields, rings, and semirings.