Back Goldener Schnitt ALS نسبة ذهبية Arabic النسبه الدهبيه ARZ Númberu aureu AST Qızıl bölgü Azerbaijani Алтын киҫелеш Bashkir Goidna Schnidd BAR Залатое сячэнне Byelorussian Залатое сечыва BE-X-OLD Златно сечение Bulgarian

Golden ratio

For other uses, see Golden ratio (disambiguation) and Golden number (disambiguation).

Golden ratio (φ)
two line segments of lengths a and b in the golden ratio: a + b is to a as a is to b
Representations
Decimal1.618033988749894...[1]
Algebraic form
Continued fraction
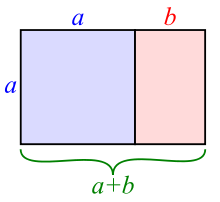
A golden rectangle with long side a + b and short side a can be divided into two pieces: a similar golden rectangle (shaded red, right) with long side a and short side b and a square (shaded blue, left) with sides of length a. This illustrates the relationship ⁠a + b/a⁠ = ⁠a/b⁠ = φ.

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if

where the Greek letter phi ( or ) denotes the golden ratio.[a] The constant satisfies the quadratic equation and is an irrational number with a value of[1]

1.618033988749....

The golden ratio was called the extreme and mean ratio by Euclid,[2] and the divine proportion by Luca Pacioli;[3] and also goes by other names.[b]

Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron.[7] A golden rectangle—that is, a rectangle with an aspect ratio of —may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural objects and artificial systems such as financial markets, in some cases based on dubious fits to data.[8] The golden ratio appears in some patterns in nature, including the spiral arrangement of leaves and other parts of vegetation.

Some 20th-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio, believing it to be aesthetically pleasing. These uses often appear in the form of a golden rectangle.

  1. ^ a b Cite error: The named reference a001622 was invoked but never defined (see the help page).
  2. ^ Cite error: The named reference Elements 6.3 was invoked but never defined (see the help page).
  3. ^ Cite error: The named reference Pacioli was invoked but never defined (see the help page).
  4. ^ Livio 2002, pp. 3, 81.
  5. ^ Cite error: The named reference goldencut was invoked but never defined (see the help page).
  6. ^ Herz-Fischler 1998.
  7. ^ Herz-Fischler 1998, pp. 20–25.
  8. ^ Cite error: The named reference strogatz nytimes was invoked but never defined (see the help page).


Cite error: There are <ref group=lower-alpha> tags or {{efn}} templates on this page, but the references will not show without a {{reflist|group=lower-alpha}} template or {{notelist}} template (see the help page).

Developed by StudentB