Hypergraph

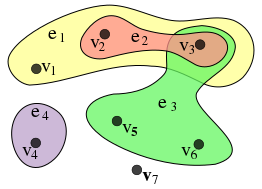
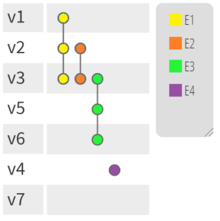
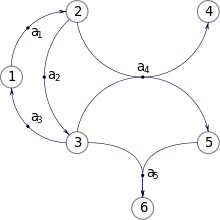
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices.

Formally, a directed hypergraph is a pair ${\displaystyle (X,E)}$, where ${\displaystyle X}$ is a set of elements called nodes, vertices, points, or elements and ${\displaystyle E}$ is a set of pairs of subsets of ${\displaystyle X}$. Each of these pairs ${\displaystyle (D,C)\in E}$ is called an edge or hyperedge; the vertex subset ${\displaystyle D}$ is known as its tail or domain, and ${\displaystyle C}$ as its head or codomain.

The order of a hypergraph ${\displaystyle (X,E)}$ is the number of vertices in ${\displaystyle X}$. The size of the hypergraph is the number of edges in ${\displaystyle E}$. The order of an edge ${\displaystyle e=(D,C)}$ in a directed hypergraph is ${\displaystyle |e|=(|D|,|C|)}$: that is, the number of vertices in its tail followed by the number of vertices in its head.

The definition above generalizes from a directed graph to a directed hypergraph by defining the head or tail of each edge as a set of vertices (${\displaystyle C\subseteq X}$ or ${\displaystyle D\subseteq X}$) rather than as a single vertex. A graph is then the special case where each of these sets contains only one element. Hence any standard graph theoretic concept that is independent of the edge orders ${\displaystyle |e|}$ will generalize to hypergraph theory.

An undirected hypergraph ${\displaystyle (X,E)}$ is an undirected graph whose edges connect not just two vertices, but an arbitrary number.^[2] An undirected hypergraph is also called a set system or a family of sets drawn from the universal set.

Hypergraphs can be viewed as incidence structures. In particular, there is a bipartite "incidence graph" or "Levi graph" corresponding to every hypergraph, and conversely, every bipartite graph can be regarded as the incidence graph of a hypergraph when it is 2-colored and it is indicated which color class corresponds to hypergraph vertices and which to hypergraph edges.

Hypergraphs have many other names. In computational geometry, an undirected hypergraph may sometimes be called a range space and then the hyperedges are called ranges.^[3] In cooperative game theory, hypergraphs are called simple games (voting games); this notion is applied to solve problems in social choice theory. In some literature edges are referred to as hyperlinks or connectors.^[4]

The collection of hypergraphs is a category with hypergraph homomorphisms as morphisms.