
Back Lorentzkrag Afrikaans قوة لورنتس Arabic Fuercia de Lorentz AST Lorens qüvvəsi Azerbaijani Сіла Лорэнца Byelorussian Сіла Лёрэнца BE-X-OLD Сила на Лоренц Bulgarian লোরেন্ৎস বল Bengali/Bangla Força de Lorentz Catalan Lorentzova síla Czech
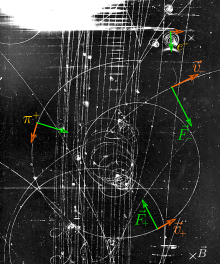
In physics, specifically in electromagnetism, the Lorentz force law is the combination of electric and magnetic force on a point charge due to electromagnetic fields. The Lorentz force, on the other hand, is a physical effect that occurs in the vicinity of electrically neutral, current-carrying conductors causing moving electrical charges to experience a magnetic force.
The Lorentz force law states that a particle of charge q moving with a velocity v in an electric field E and a magnetic field B experiences a force (in SI units[1][2]) of It says that the electromagnetic force on a charge q is a combination of (1) a force in the direction of the electric field E (proportional to the magnitude of the field and the quantity of charge), and (2) a force at right angles to both the magnetic field B and the velocity v of the charge (proportional to the magnitude of the field, the charge, and the velocity).
Variations on this basic formula describe the magnetic force on a current-carrying wire (sometimes called Laplace force), the electromotive force in a wire loop moving through a magnetic field (an aspect of Faraday's law of induction), and the force on a moving charged particle.[3]
Historians suggest that the law is implicit in a paper by James Clerk Maxwell, published in 1865.[4] Hendrik Lorentz arrived at a complete derivation in 1895,[5] identifying the contribution of the electric force a few years after Oliver Heaviside correctly identified the contribution of the magnetic force.[6]
- ^ In SI units, B is measured in teslas (symbol: T). In Gaussian-cgs units, B is measured in gauss (symbol: G). See e.g. "Geomagnetism Frequently Asked Questions". National Geophysical Data Center. Retrieved 21 October 2013.)
- ^ H is measured in amperes per metre (A/m) in SI units, and in oersteds (Oe) in cgs units. "International system of units (SI)". NIST reference on constants, units, and uncertainty. National Institute of Standards and Technology. 12 April 2010. Retrieved 9 May 2012.
- ^ Huray, Paul G. (2009-11-16). Maxwell's Equations. John Wiley & Sons. ISBN 978-0-470-54276-7.
- ^ Cite error: The named reference
Huraywas invoked but never defined (see the help page). - ^ Cite error: The named reference
Dahlwas invoked but never defined (see the help page). - ^ Cite error: The named reference
Nahinwas invoked but never defined (see the help page).
