
Back تآلف صغير Arabic Acord menor Catalan Mollový kvintakord Czech Molldreiklang German Minoorkolmkõla Estonian آکورد مینور Persian Accord parfait mineur French אקורד מינורי HE 短三和音 Japanese 단3화음 Korean
| Component intervals from root | |
|---|---|
| perfect fifth | |
| minor third | |
| root | |
| Tuning | |
| 10:12:15[1] | |
| Forte no. / | |
| 3-11 / |
In music theory, a minor chord is a chord that has a root, a minor third, and a perfect fifth.[2] When a chord comprises only these three notes, it is called a minor triad. For example, the minor triad built on A, called an A minor triad, has pitches A–C–E:
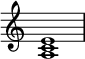

In harmonic analysis and on lead sheets, a C minor chord can be notated as Cm, C−, Cmin, or simply the lowercase "c". A minor triad is represented by the integer notation {0, 3, 7}.
A minor triad can also be described by its intervals: the interval between the bottom and middle notes is a minor third, and the interval between the middle and top notes is a major third. By contrast, a major triad has a major third on the bottom and minor third on top. They both contain fifths, because a minor third (three semitones) plus a major third (four semitones) equals a perfect fifth (seven semitones). Chords that are constructed of consecutive (or "stacked") thirds are called tertian.
In Western classical music from 1600 to 1820 and in Western pop, folk and rock music, a major chord is usually played as a triad. Along with the major triad, the minor triad is one of the basic building blocks of tonal music and the common practice period. In Western music, a minor chord, in comparison, "sounds darker than a major chord"[3] but is still considered highly consonant, stable, or as not requiring resolution.
Some minor chords with additional notes, such as the minor seventh chord, may also be called minor chords.
- ^ Shirlaw, Matthew (16 June 2015). The Theory of Harmony. p. 81. ISBN 978-1-4510-1534-8.
20:24:30
- ^ Miller, Michael (2005). The Complete Idiot's Guide to Music Theory (2nd ed.). Indianapolis: Alpha. p. 114. ISBN 1-59257-437-8.
- ^ Kamien, Roger (2008). Music: An Appreciation (6th brief ed.). p. 46. ISBN 978-0-07-340134-8.