Back Distribució multimodal Catalan Distribution multimodale French 다봉분포 Korean Bimodal distribution SIMPLE Мультимодальний розподіл Ukrainian 雙峰分布 Chinese

Multimodal distribution

"Bimodal" redirects here. For the musical concept, see Bimodality.
Figure 1. A simple bimodal distribution, in this case a mixture of two normal distributions with the same variance but different means. The figure shows the probability density function (p.d.f.), which is an equally-weighted average of the bell-shaped p.d.f.s of the two normal distributions. If the weights were not equal, the resulting distribution could still be bimodal but with peaks of different heights.
Figure 2. A bimodal distribution.
Figure 3. A bivariate, multimodal distribution
A 3D plot of a probability distribution. It ripples and spirals away from the origin, with only one local maximum near the origin.
Figure 4. A non-example: a unimodal distribution, that would become multimodal if conditioned on either x or y.

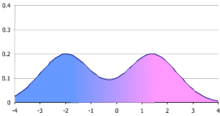
In statistics, a multimodal distribution is a probability distribution with more than one mode (i.e., more than one local peak of the distribution). These appear as distinct peaks (local maxima) in the probability density function, as shown in Figures 1 and 2. Categorical, continuous, and discrete data can all form multimodal distributions. Among univariate analyses, multimodal distributions are commonly bimodal.[citation needed]

Developed by StudentB