Orientability

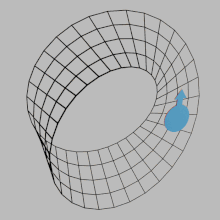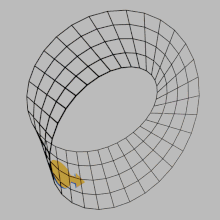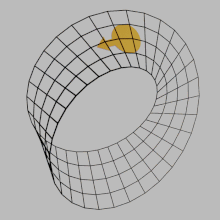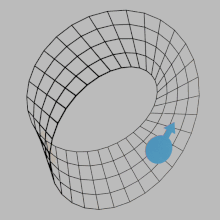
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "anticlockwise".^[1] A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space.

Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds often employ methods of homology theory, whereas for differentiable manifolds more structure is present, allowing a formulation in terms of differential forms. A generalization of the notion of orientability of a space is that of orientability of a family of spaces parameterized by some other space (a fiber bundle) for which an orientation must be selected in each of the spaces which varies continuously with respect to changes in the parameter values.