
Back فرط الملاءمة Arabic Sobreajustament (overfitting) Catalan Overfitting Czech Überanpassung German Sobreajuste Spanish بیشبرازش Persian Surapprentissage French התאמת יתר HE Overfitting ID Overfitting Italian
This article needs additional citations for verification. (August 2017) |
| Part of a series on |
| Machine learning and data mining |
|---|


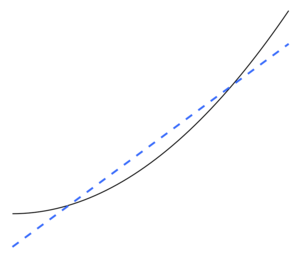
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably".[1] An overfitted model is a mathematical model that contains more parameters than can be justified by the data.[2] In a mathematical sense, these parameters represent the degree of a polynomial. The essence of overfitting is to have unknowingly extracted some of the residual variation (i.e., the noise) as if that variation represented underlying model structure.[3]: 45
Underfitting occurs when a mathematical model cannot adequately capture the underlying structure of the data. An under-fitted model is a model where some parameters or terms that would appear in a correctly specified model are missing.[2] Underfitting would occur, for example, when fitting a linear model to nonlinear data. Such a model will tend to have poor predictive performance.
The possibility of over-fitting exists because the criterion used for selecting the model is not the same as the criterion used to judge the suitability of a model. For example, a model might be selected by maximizing its performance on some set of training data, and yet its suitability might be determined by its ability to perform well on unseen data; overfitting occurs when a model begins to "memorize" training data rather than "learning" to generalize from a trend.
As an extreme example, if the number of parameters is the same as or greater than the number of observations, then a model can perfectly predict the training data simply by memorizing the data in its entirety. (For an illustration, see Figure 2.) Such a model, though, will typically fail severely when making predictions.
Overfitting is directly related to approximation error of the selected function class and the optimization error of the optimization procedure. A function class that is too large, in a suitable sense, relative to the dataset size is likely to overfit.[4] Even when the fitted model does not have an excessive number of parameters, it is to be expected that the fitted relationship will appear to perform less well on a new dataset than on the dataset used for fitting (a phenomenon sometimes known as shrinkage).[2] In particular, the value of the coefficient of determination will shrink relative to the original data.
To lessen the chance or amount of overfitting, several techniques are available (e.g., model comparison, cross-validation, regularization, early stopping, pruning, Bayesian priors, or dropout). The basis of some techniques is to either (1) explicitly penalize overly complex models or (2) test the model's ability to generalize by evaluating its performance on a set of data not used for training, which is assumed to approximate the typical unseen data that a model will encounter.
- ^ Definition of "overfitting" at OxfordDictionaries.com: this definition is specifically for statistics.
- ^ a b c Everitt B.S., Skrondal A. (2010), Cambridge Dictionary of Statistics, Cambridge University Press.
- ^ Cite error: The named reference
BA2002was invoked but never defined (see the help page). - ^ Bottou, Léon; Bousquet, Olivier (2011-09-30), "The Tradeoffs of Large-Scale Learning", Optimization for Machine Learning, The MIT Press, pp. 351–368, doi:10.7551/mitpress/8996.003.0015, ISBN 978-0-262-29877-3, retrieved 2023-12-08