
Back Parsek Afrikaans Pársec AN فرسخ فلكي Arabic Pársec AST Parsek Azerbaijani Парсек Byelorussian Парсэк BE-X-OLD Парсек Bulgarian পারসেক Bengali/Bangla Parsek BS
| Parsec | |
|---|---|
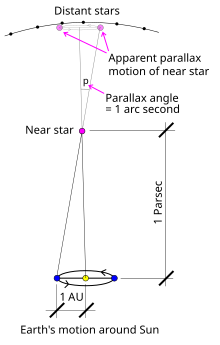 A parsec is the distance from the Sun to an astronomical object that has a parallax angle of one arcsecond (not to scale) | |
| General information | |
| Unit system | astronomical units |
| Unit of | length/distance |
| Symbol | pc |
| Conversions | |
| 1 pc in ... | ... is equal to ... |
| metric (SI) units | 3.0857×1016 m ≈31 petametres |
| imperial US units | 1.9174×1013 mi |
| astronomical units | 206,265 au 3.26156 ly |
The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to 3.26 light-years or 206,265 astronomical units (AU), i.e. 30.9 trillion kilometres (19.2 trillion miles).[a] The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 AU subtends an angle of one arcsecond[1] (1/3600 of a degree). The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun: from that distance, the gap between the Earth and the Sun spans slightly less than 1/3600 of one degree of view.[2] Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand parsecs, and the Andromeda Galaxy at over 700,000 parsecs.[3]
The word parsec is a portmanteau of "parallax of one second" and was coined by the British astronomer Herbert Hall Turner in 1913[4] to simplify astronomers' calculations of astronomical distances from only raw observational data. Partly for this reason, it is the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and common usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs (kpc) for the more distant objects within and around the Milky Way, megaparsecs (Mpc) for mid-distance galaxies, and gigaparsecs (Gpc) for many quasars and the most distant galaxies.
In August 2015, the International Astronomical Union (IAU) passed Resolution B2 which, as part of the definition of a standardized absolute and apparent bolometric magnitude scale, mentioned an existing explicit definition of the parsec as exactly 648000/π au, or approximately 3.0856775814913673×1016 metres (based on the IAU 2012 definition of the astronomical unit). This corresponds to the small-angle definition of the parsec found in many astronomical references.[5][6]
Cite error: There are <ref group=lower-alpha> tags or {{efn}} templates on this page, but the references will not show without a {{reflist|group=lower-alpha}} template or {{notelist}} template (see the help page).
- ^ "Cosmic Distance Scales – The Milky Way". Retrieved 24 September 2014.
- ^ Benedict, G. F.; et al. "Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri" (PDF). Proceedings of the HST Calibration Workshop. pp. 380–384. Retrieved 11 July 2007.
- ^ "Farthest Stars". StarDate. University of Texas at Austin. 15 May 2021. Retrieved 5 September 2021.
- ^ Dyson, F. W. (March 1913). "The distribution in space of the stars in Carrington's Circumpolar Catalogue". Monthly Notices of the Royal Astronomical Society. 73 (5): 342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334.
[paragraph 14, page 342] Taking the unit of distance R* to be that corresponding to a parallax of 1″·0 [… Footnote:]
* There is need for a name for this unit of distance. Mr. Charlier has suggested Siriometer, but if the violence to the Greek language can be overlooked, the word Astron might be adopted. Professor Turner suggests Parsec, which may be taken as an abbreviated form of "a distance corresponding to a parallax of one second". - ^ Cox, Arthur N., ed. (2000). Allen's Astrophysical Quantities (4th ed.). New York: AIP Press / Springer. Bibcode:2000asqu.book.....C. ISBN 978-0387987460.
- ^ Binney, James; Tremaine, Scott (2008). Galactic Dynamics (2nd ed.). Princeton, NJ: Princeton University Press. Bibcode:2008gady.book.....B. ISBN 978-0-691-13026-2.