
Back ثلاثية فيثاغورس Arabic Піфагорава тройка Byelorussian Пітагорава тройка BE-X-OLD Питагоров триъгълник Bulgarian Pitagorine trojke BS Terna pitagòrica Catalan سیانەی پیتاگۆرسی CKB Pythagorejská trojice Czech Triawdau Pythagoraidd Welsh Pythagoræiske tal Danish
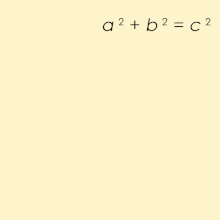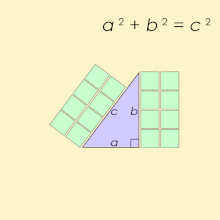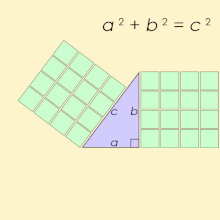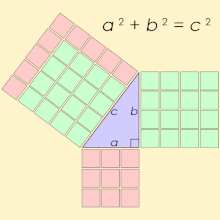
A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A triangle whose side lengths are a Pythagorean triple is a right triangle and called a Pythagorean triangle.
A primitive Pythagorean triple is one in which a, b and c are coprime (that is, they have no common divisor larger than 1).[1] For example, (3, 4, 5) is a primitive Pythagorean triple whereas (6, 8, 10) is not. Every Pythagorean triple can be scaled to a unique primitive Pythagorean triple by dividing (a, b, c) by their greatest common divisor. Conversely, every Pythagorean triple can be obtained by multiplying the elements of a primitive Pythagorean triple by a positive integer (the same for the three elements).
The name is derived from the Pythagorean theorem, stating that every right triangle has side lengths satisfying the formula ; thus, Pythagorean triples describe the three integer side lengths of a right triangle. However, right triangles with non-integer sides do not form Pythagorean triples. For instance, the triangle with sides and is a right triangle, but is not a Pythagorean triple because the square root of 2 is not an integer or ratio of integers. Moreover, and do not have an integer common multiple because is irrational.
Pythagorean triples have been known since ancient times. The oldest known record comes from Plimpton 322, a Babylonian clay tablet from about 1800 BC, written in a sexagesimal number system.[2]
When searching for integer solutions, the equation a2 + b2 = c2 is a Diophantine equation. Thus Pythagorean triples are among the oldest known solutions of a nonlinear Diophantine equation.
- ^ Long (1972, p. 48)
- ^ Robson, Eleanor (2002), "Words and Pictures: New Light on Plimpton 322" (PDF), The American Mathematical Monthly, 109 (2): 105–120, doi:10.1080/00029890.2002.11919845, S2CID 33907668





