Quadratic function

In mathematics, a quadratic function of a single variable is a function of the form^[1]

${\displaystyle f(x)=ax^{2}+bx+c,\quad a\neq 0,}$

where ⁠${\displaystyle x}$⁠ is its variable, and ⁠${\displaystyle a}$⁠, ⁠${\displaystyle b}$⁠, and ⁠${\displaystyle c}$⁠ are coefficients. The expression ⁠${\displaystyle \textstyle ax^{2}+bx+c}$⁠, especially when treated as an object in itself rather than as a function, is a quadratic polynomial, a polynomial of degree two. In elementary mathematics a polynomial and its associated polynomial function are rarely distinguished and the terms quadratic function and quadratic polynomial are nearly synonymous and often abbreviated as quadratic.

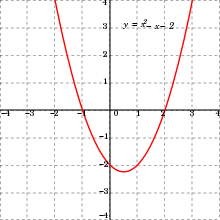
The graph of a real single-variable quadratic function is a parabola. If a quadratic function is equated with zero, then the result is a quadratic equation. The solutions of a quadratic equation are the zeros (or roots) of the corresponding quadratic function, of which there can be two, one, or zero. The solutions are described by the quadratic formula.

A quadratic polynomial or quadratic function can involve more than one variable. For example, a two-variable quadratic function of variables ⁠${\displaystyle x}$⁠ and ⁠${\displaystyle y}$⁠ has the form

${\displaystyle f(x,y)=ax^{2}+bxy+cy^{2}+dx+ey+f,}$

with at least one of ⁠${\displaystyle a}$⁠, ⁠${\displaystyle b}$⁠, and ⁠${\displaystyle c}$⁠ not equal to zero. In general the zeros of such a quadratic function describe a conic section (a circle or other ellipse, a parabola, or a hyperbola) in the ⁠${\displaystyle x}$⁠–⁠${\displaystyle y}$⁠ plane. A quadratic function can have an arbitrarily large number of variables. The set of its zero form a quadric, which is a surface in the case of three variables and a hypersurface in general case.