
Back Subdifferential German Sous-différentiel French Subdifferenziale Italian 劣微分 Japanese 하방미분 Korean Subróżniczka Polish Subderivada Portuguese Субдифференциал Russian Subgradient Swedish Субдиференціал Ukrainian
In mathematics, subderivatives (or subgradient) generalizes the derivative to convex functions which are not necessarily differentiable. The set of subderivatives at a point is called the subdifferential at that point.[1] Subderivatives arise in convex analysis, the study of convex functions, often in connection to convex optimization.
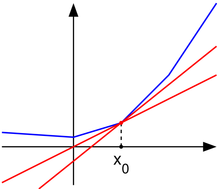
Let be a real-valued convex function defined on an open interval of the real line. Such a function need not be differentiable at all points: For example, the absolute value function is non-differentiable when . However, as seen in the graph on the right (where in blue has non-differentiable kinks similar to the absolute value function), for any in the domain of the function one can draw a line which goes through the point and which is everywhere either touching or below the graph of f. The slope of such a line is called a subderivative.
- ^ Bubeck, S. (2014). Theory of Convex Optimization for Machine Learning. ArXiv, abs/1405.4980.





