Back Sudoku Afrikaans Sudoku AN سودوكو Arabic Sudoku AST Sudoku Azerbaijani Судоку Bashkir Судоку Bulgarian Sudoku Breton Sudoku BS Sudoku Catalan

Sudoku

Not to be confused with Sodoku (the disease).

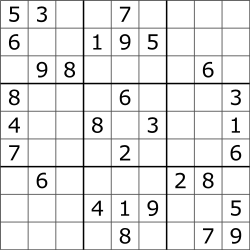
A typical Sudoku puzzle, with nine rows and nine columns that intersect at square spaces. Some of the cells are filled with a number; others are blank cells to be solved.
A typical Sudoku puzzle
The previous puzzle, showing its solution.
The solution to the puzzle above

Sudoku (/suːˈdoʊkuː, -ˈdɒk-, sə-/; Japanese: 数独, romanized: sūdoku, lit. 'digit-single'; originally called Number Place)[1] is a logic-based,[2][3] combinatorial[4] number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid (also called "boxes", "blocks", or "regions") contains all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.

French newspapers featured variations of the Sudoku puzzles in the 19th century, and the puzzle has appeared since 1979 in puzzle books under the name Number Place.[5] However, the modern Sudoku only began to gain widespread popularity in 1986 when it was published by the Japanese puzzle company Nikoli under the name Sudoku, meaning "single number".[6] It first appeared in a U.S. newspaper, and then The Times (London), in 2004, thanks to the efforts of Wayne Gould, who devised a computer program to rapidly produce unique puzzles.

  1. ^ Grossman, Lev (Mar 11, 2013). "The Answer Men". Time. New York. Archived from the original on 2013-03-01. Retrieved 2013-03-04.(registration required)
  2. ^ Arnoldy, Ben. "Sudoku Strategies". The Christian Science Monitor.
  3. ^ Schaschek, Sarah (Mar 22, 2006). "Sudoku champ's surprise victory". The Prague Post. Archived from the original on 2006-08-13. Retrieved 2009-02-18.
  4. ^ Gradwohl, Ronen; Naor, Moni; Pinkas, Benny; Rothblum, Guy N. (2007). "Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles". In Crescenzi, Pierluigi; Prencipe, Giuseppe; Pucci, Geppino (eds.). Fun with Algorithms, 4th International Conference, FUN 2007, Castiglioncello, Italy, June 3-5, 2007, Proceedings. Lecture Notes in Computer Science. Vol. 4475. Springer. pp. 166–182. doi:10.1007/978-3-540-72914-3_16. ISBN 978-3-540-72913-6.
  5. ^ Cite error: The named reference Smith was invoked but never defined (see the help page).
  6. ^ Hayes, Brian (2006). "Unwed Numbers". American Scientist. 94 (1): 12–15. doi:10.1511/2006.57.3475.

Developed by StudentB