
Back Ortobicúpula triangular Catalan Disheptaeder German Triangula ortodukupolo Esperanto Ortobicúpula triangular Spanish Ortobikupula triangeluar Basque Orthobicoupole hexagonale French Ortobicupola triangolare Italian 同相双三角台塔 Japanese Gedraaide kuboctaëder Dutch Ortobicúpula triangular Portuguese
| Triangular orthobicupola | |
|---|---|
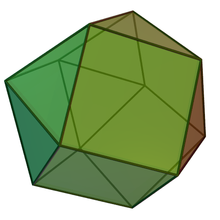 | |
| Type | Johnson J26 – J27 – J28 |
| Faces | 2+6 triangles 6 squares |
| Edges | 24 |
| Vertices | 12 |
| Vertex configuration | 6(32.42) 6(3.4.3.4) |
| Symmetry group | D3h |
| Dual polyhedron | Trapezo-rhombic dodecahedron |
| Properties | convex |
| Net | |
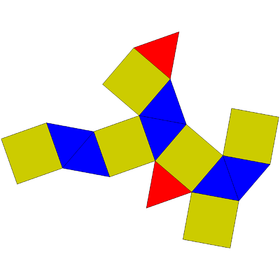 | |
In geometry, the triangular orthobicupola is one of the Johnson solids (J27). As the name suggests, it can be constructed by attaching two triangular cupolas (J3) along their bases. It has an equal number of squares and triangles at each vertex; however, it is not vertex-transitive. It is also called an anticuboctahedron, twisted cuboctahedron or disheptahedron. It is also a canonical polyhedron.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
The triangular orthobicupola is the first in an infinite set of orthobicupolae.
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.