
Back Raketengrundgleichung ALS معادلة تسالكوفسكي الصاروخية Arabic Формула на Циолковски Bulgarian Equació de Tsiolkovski Catalan Ciolkovského rovnice Czech Raketligningen Danish Raketengrundgleichung German Ecuación del cohete de Tsiolkovski Spanish Tsiolkovskin laki Finnish Équation de Tsiolkovski French
| Part of a series on |
| Astrodynamics |
|---|
The classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity and can thereby move due to the conservation of momentum. It is credited to Konstantin Tsiolkovsky, who independently derived it and published it in 1903,[1][2] although it had been independently derived and published by William Moore in 1810,[3] and later published in a separate book in 1813.[4] Robert Goddard also developed it independently in 1912, and Hermann Oberth derived it independently about 1920.
The maximum change of velocity of the vehicle, (with no external forces acting) is:
where:
- is the effective exhaust velocity;
- is the specific impulse in dimension of time;
- is standard gravity;
- is the natural logarithm function;
- is the initial total mass, including propellant, a.k.a. wet mass;
- is the final total mass without propellant, a.k.a. dry mass.
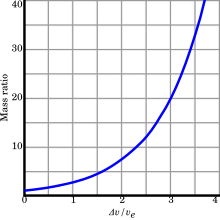
Given the effective exhaust velocity determined by the rocket motor's design, the desired delta-v (e.g., orbital speed or escape velocity), and a given dry mass , the equation can be solved for the required propellant mass :
The necessary wet mass grows exponentially with the desired delta-v.
- ^ К. Ціолковскій, Изслѣдованіе мировыхъ пространствъ реактивными приборами, 1903 (available online here Archived 2011-08-15 at the Wayback Machine in a RARed PDF)
- ^ Tsiolkovsky, K. "Reactive Flying Machines" (PDF).
- ^ Moore, William (1810). "On the Motion of Rockets both in Nonresisting and Resisting Mediums". Journal of Natural Philosophy, Chemistry & the Arts. 27: 276–285.
- ^ Moore, William (1813). A Treatise on the Motion of Rockets: to which is added, an Essay on Naval Gunnery, in theory and practice, etc. G. & S. Robinson.









