
Back دوال مثلثية عكسية Arabic Tərs triqonometrik funksiyalar Azerbaijani Кире тригонометрик функциялар Bashkir Обратни тригонометрични функции Bulgarian বিপরীত ত্রিকোণমিতিক অপেক্ষক Bengali/Bangla Inverses de les funcions trigonomètriques Catalan فانکشنە سێگۆشەیییە ھەڵگەڕاوەکان CKB Cyklometrická funkce Czech Тригонометрилле кутăнла функцисем CV Arcus-funktioner Danish
| Matematikaj funkcioj |
|---|
| Aroj: fonta aro, argumentaro, bildaro, cela aro (suma klarigo) • malbildo |
| Fundamentaj funkcioj |
| Algebraj funkcioj: konstanta • lineara • kvadrata • polinoma • racionala • Transformo de Möbius Aliaj funkcioj: trigonometriaj • inversa trigonometria • hiperbola • eksponenta • logaritma • potenca |
| Specialaj funkcioj |
| erara • β • Γ • ζ • η • W de Lambert • de Bessel |
| Nombroteoriaj funkcioj: |
| τ • σ • de Möbius • φ • π • λ |
| Ecoj: |
| totaleco kaj parteco • pareco kaj malpareco • monotoneco • bariteco • periodeco • disĵeteco • surĵeteco • dissurĵeteco kontinueco • derivaĵeco • integralebleco |
En matematiko, la inversaj trigonometriaj funkcioj estas la retroĵetoj de la trigonometriaj funkcioj. La ĉefaj estas jenaj:
| Nomo | Kutima skribmaniero | Difino | Argumentaro de x por reela rezulto | Bildaro |
|---|---|---|---|---|
| Sinusarko | y = arcsin(x) | x = sin(y) | −1 ≤ x ≤ 1 | −π/2 ≤ y ≤ π/2 |
| Kosinusarko | y = arccos(x) | x = cos(y) | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π |
| Tangentarko | y = arctan(x) aŭ y = arctg(x) |
x = tan(y) | ĉiuj reelaj x | −π/2 < y < π/2 |
| Kotangentarko | y = arccot(x) aŭ y = arccotan(x) aŭ y = arcctg(x) |
x = cot(y) | ĉiuj reelaj x | 0 < y < π |
| Sekantarko | y = arcsec(x) | x = sec(y) | −∞ < x ≤ −1 aŭ 1 ≤ x < ∞ | 0 ≤ y < π/2 aŭ π/2 < y ≤ π |
| Kosekantarko | y = arccsc(x) aŭ y = arccosec(x) |
x = csc(y) | −∞ < x ≤ −1 aŭ 1 ≤ x < ∞ | −π/2 ≤ y < 0 aŭ 0 < y ≤ π/2 |
Se x estas permesita al esti kompleksa nombro, tiam la supre donitaj limigoj de y aplikas nur al reelaj x.
La skribmaniero sin−1, cos−1, ktp estas ofte uzata por arcsin, arccos, ktp.
 La kutimaj ĉefaj valoroj de la arcsin(x) kaj arccos(x) |
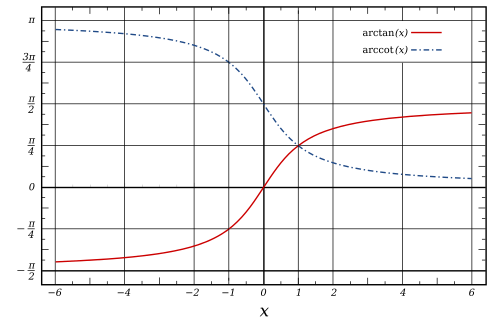 La kutimaj ĉefaj valoroj de la arctan(x) kaj arccot(x) |
 La kutimaj ĉefaj valoroj de la arcsec(x) kaj arccsc(x) |
En komputilaj programlingvoj la funkcioj arcsin, arccos, arctan estas kutime nomataj kiel asin, acos, atan. Multaj programlingvoj ankaŭ provizas la du-argumentan funkcion atan2, vidu sube pri ĝi.