
Back مرجح Arabic Baricentru AST সাধারণ ভরকেন্দ্র (জ্যোতির্বিজ্ঞান) Bengali/Bangla Barycentrum Czech Барицентр CV Barycentrum Danish Baryzentrum German Barycenter (astronomy) English مرکز سنگینی سراسری Persian Baricentro (astronomía) Galician
En física, el baricentro de un cuerpo material coincide con el centro de masas del mismo cuando el cuerpo es homogéneo (densidad uniforme) o cuando la distribución de materia en el cuerpo tiene ciertas propiedades, tales como la simetría. Se distingue del centroide en geometría, donde el baricentro de una superficie contenida en una figura geométrica plana es un punto tal que cualquier recta que pasa por él divide a dicho segmento en dos partes de igual momento respecto a dicha recta.
Si uno de los dos cuerpos en órbita es mucho más masivo que el otro y los cuerpos están relativamente cerca uno del otro, el baricentro normalmente se ubicará dentro del objeto más masivo. En este caso, en lugar de que los dos cuerpos parezcan orbitar alrededor de un punto entre ellos, el cuerpo menos masivo parecerá orbitar alrededor del cuerpo más masivo, mientras que se puede observar que el cuerpo más masivo se tambalea ligeramente. Este es el caso del sistema Tierra-Luna, cuyo baricentro se encuentra en promedio a 4671 kilómetros (2902,4 mi) del centro de la Tierra, que es el 75% del radio de la Tierra de 6378 kilómetros (3963,1 mi).
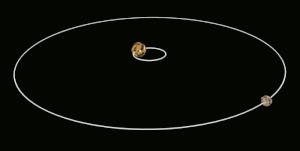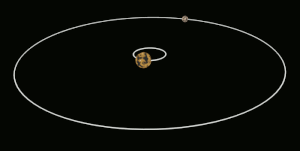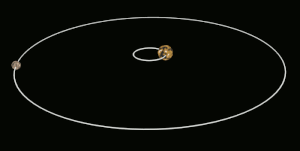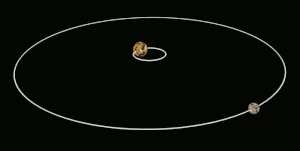
Cuando los dos cuerpos son de masas similares, el baricentro generalmente se ubicará en un punto entre ellos y ambos cuerpos orbitarán alrededor de él. Este es el caso de Plutón y Caronte, uno de los satélites naturales de Plutón, así como de muchos asteroides binarios y estrellas binarias. Cuando el objeto menos masivo está lejos, el baricentro puede ubicarse fuera del objeto más masivo. Este es el caso de Júpiter y el Sol; a pesar de que el Sol es mil veces más masivo que Júpiter, su baricentro está ligeramente fuera del Sol debido a la distancia relativamente grande entre ellos.[1]
- ↑ MacDougal, Douglas W. (December 2012). Newton's Gravity: An Introductory Guide to the Mechanics of the Universe. Berlin: Springer Science & Business Media. p. 199. ISBN 978-1-4614-5444-1.