
Back مجسم المعين المنحرف Arabic Trapezoeder German Trapezohedron English Kajtopluredro Esperanto Trapezoedro Spanish Trapezoedro Basque Trapézoèdre French Trapezoedro IO Trapezoedro Italian ねじれ双角錐 Japanese
| Trapetsoedrit | |
|---|---|
| |
| Conwayn merkintä | dAn |
| Schläflin symboli | { } ⨁ {n}[1] |
| Coxeterin diagrammit | |
| Tahkoja | 2n leijaa |
| Särmiä | 4n |
| Kärkiä | 2n + 2 |
| Tahkokonfiguraatio | V3.3.3.n |
| Symmetriaryhmä | Dnd, [2+,2n], (2*n), kertalukua 4n |
| Rotaatioryhmä | Dn, [2,n]+, (22n), kertalukua 2n |
| Duaalikappale | antiprisma |
| Ominaisuudet | kupera, tahkotransitiivinen |
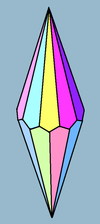
n-kulmainen trapetsoedri, antidipyramidi, antibipyramidi eli deltoedri on avaruusgeometriassa n-kulmaisen antiprisman duaalikappale.[2] Symmetrisimmillä trapetsoedreilla on tahkoinaan 2n keskenään yhtenevää leijaa, joita sanotaan myös trapetseiksi eli deltoideiksi. Tahkot sijaitsevat symmetrisesti kappaleen akselin ympärillä.
Luku n, jonka mukaan trapetsoeria nimitetään n-kulmaiseksi, ei tarkoita, että tahkot olisivat n-kulmioita, sillä ne ovat aina nelikulmioita. Sen sijaan luku viittaa kärkien sijoittumiseen kappaleen symmetria-akselin ympärillä. Sen sijaan n-kulmaisella antiprismalla todella on tahkoina kaksi n-kulmiota.
n-kulmainen trapetsoedri voidaan jakaa kahdeksi yhteneväksi n-kulmaiseksi pyramidiksi sekä yhdeksi n-kulmaiseksi antiprismaksi.
- ↑ Norman Johnson: ”Chapter 11: Finite symmetry groups, 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c”, Geometries and Transformations. Cambridge University Press, 2018. ISBN 978-1-107-10340-5 (englanniksi)
- ↑ Trapezohedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 12.2.2019. (englanniksi)