Logarithme

En mathématiques, un logarithme est la fonction réciproque d'une exponentiation, c'est-à-dire que le logarithme de base $b$ d'un nombre réel strictement positif est la puissance à laquelle il faut élever la base $b$ pour obtenir ce nombre.

Exemple :

Le logarithme en base dix de 1000 est 3 car 10³ = 10×10×10 = 1000.

Dans ce cas, le plus simple, le logarithme est le nombre entier qui compte les répétitions de la base multipliée par elle-même. Dans cette opération, multiplier un nombre par la base équivaut à ajouter 1 à son logarithme. L'exponentiation généralise cette opération de multiplication par soi-même à des puissances intermédiaires entre les entiers, qu'on exprime en nombres réels.

Exemple :

Le logarithme en base dix de la racine de 10, notée ${\sqrt {10}}$ , est 0,5 car

${\sqrt {10}}^{2}={\sqrt {10}}\times {\sqrt {10}}=10$ , donc $(\log _{10}{\sqrt {10}})+(\log _{10}{\sqrt {10}})=\log _{10}{10}=1$

Le logarithme de base $b$ du nombre $x$ se note $log b x$ . Si la base est évidente d'après le contexte, ou si elle n'a pas d'importance, on peut écrire simplement $log x$ . Par définition, $b^{\log _{b}x}=x$ .

John Napier a développé les logarithmes au début du XVII^e siècle. L'utilité du logarithme pour le calcul vient du fait que la fonction logarithme transforme un produit en somme : $\log _{b}(x\cdot y)=\log _{b}x+\log _{b}y\,$ . Pendant trois siècles, la table de logarithmes et la règle à calcul, fondée sur une échelle logarithmique, ont servi pour le calcul, jusqu'à leur remplacement, dans le dernier quart du XX^e siècle, par des calculatrices électroniques.

Le logarithme permet en outre de présenter sous une forme concise des relations entre nombres d'ordre de grandeur très différents.

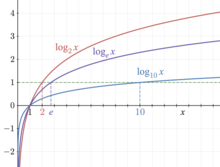
Trois fonctions logarithmes sont d'usage courant :

le logarithme népérien (ou naturel) dont la base est le nombre $e$ , est fondamental en analyse mathématique car il est la primitive de la fonction $x\mapsto {\tfrac {1}{x}}$ s’annulant en 1 et la fonction réciproque de la fonction exponentielle ; il est souvent noté $ln$ sauf en informatique ou en théorie des nombres où $log$ sans autre précision signifie en général logarithme népérien ;
le logarithme décimal, dont la base est 10, reste le plus communément utilisé pour les calculs dans le domaine technologique ainsi qu'en chimie pour le calcul de pH ;
le logarithme binaire, dont la base est 2, est utile en informatique théorique et pour certains calculs appliqués.

Le logarithme complexe généralise la notion de logarithme aux nombres complexes.