Orthogonaal

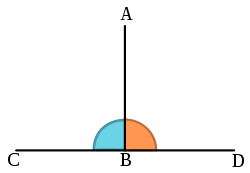
In de twee- of driedimensionale euclidische meetkunde zegt men van twee objecten dat zij orthogonaal (van Oudgrieks: ὀρθός (orthos), recht en γωνία (gonia), hoek) zijn, als zij ten opzichte van elkaar een rechte hoek vormen, of anders gezegd loodrecht (haaks) op elkaar staan. Dit wordt wel aangegeven door het teken ${\displaystyle \perp }$ tussen de objecten te plaatsen. Ook van meer dan twee objecten zegt men dat zij orthogonaal zijn, als elk tweetal van deze objecten orthogonaal is.

In andere takken van de wiskunde spreekt men ook over orthogonale objecten zonder dat er nog enig verband bestaat met het gewone begrip rechte hoek of loodrechte stand. Orthogonaliteit van objecten heeft dan een specifieke betekenis die veelal verbonden is met de aard van die objecten. Hierna volgen een paar voorbeelden.

In de statistiek wordt met de term ook wel volledige afwezigheid van correlatie tussen twee variabelen bedoeld.